class: center, middle, inverse, title-slide # Inference for regression and Central Limit Theorem ### Dr. Çetinkaya-Rundel ### November 9, 2017 --- class: center, middle # Getting started --- ## Getting started - Any questions from last time? --- ## From last time: Probabilities of testing errors - P(Type 1 error) = `\(\alpha\)` - P(Type 2 error) = 1 - Power - Power = P(correctly rejecting the null hypothesis) <div class="question"> 👥 Fill in the blanks in terms of correctly/incorrectly rejecting/failing to reject the null hypothesis: <ul> <li> `\(\alpha\)` is the probability of ___. <li> 1 - Power is the probability of ___. </ul> </div> --- class: center, middle # Inference for modeling --- ## Riders in Florence, MA <div class="question"> 👤 Interpret the coefficients of the regression model for predicting volume (estimated number of trail users that day) from hightemp (daily high temperature, in F). </div> .small[ ```r library(mosaicData) m_riders <- lm(volume ~ hightemp, data = RailTrail) m_riders$coefficients ``` ``` ## (Intercept) hightemp ## -17.079281 5.701878 ``` ] <!-- --> --- ## Uncertainty around the slope <!-- --> --- ## Bootstrapping the data, once <!-- --> --- ## Bootstrapping the data, once again <!-- --> --- ## Bootstrapping the data, again 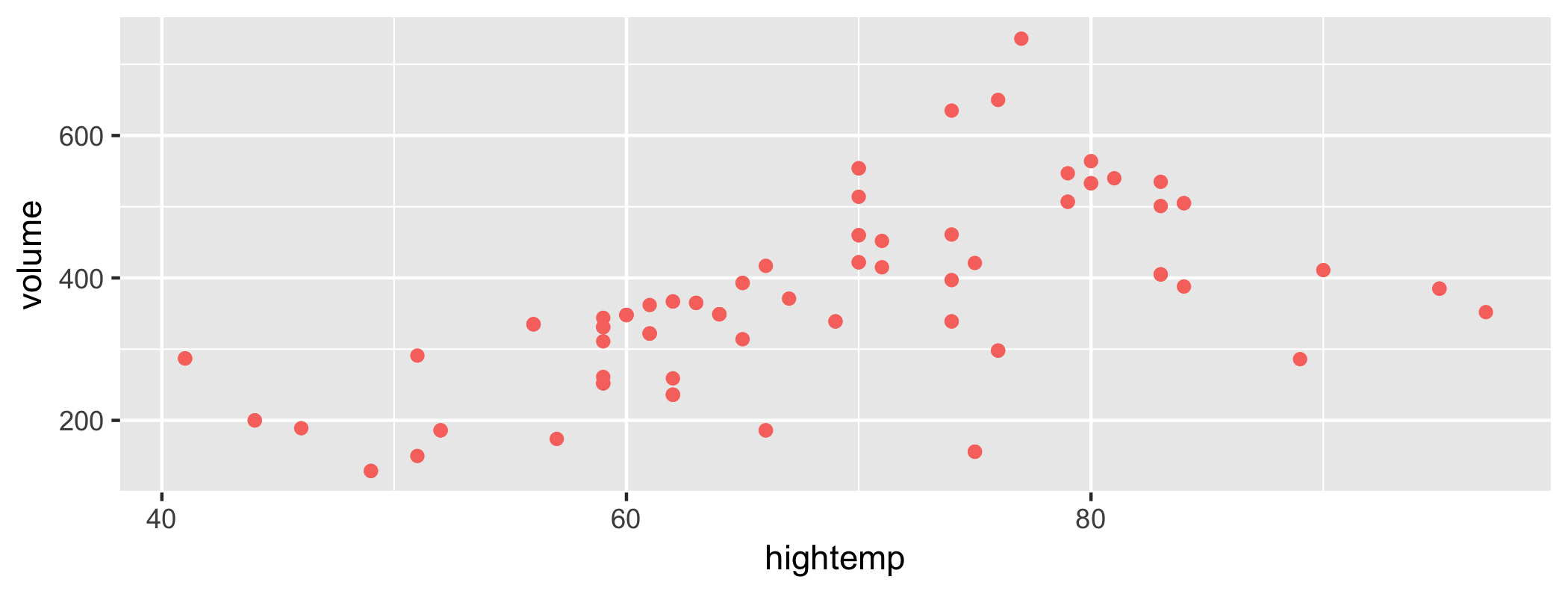<!-- --> --- ## Bootstrapping the regression line 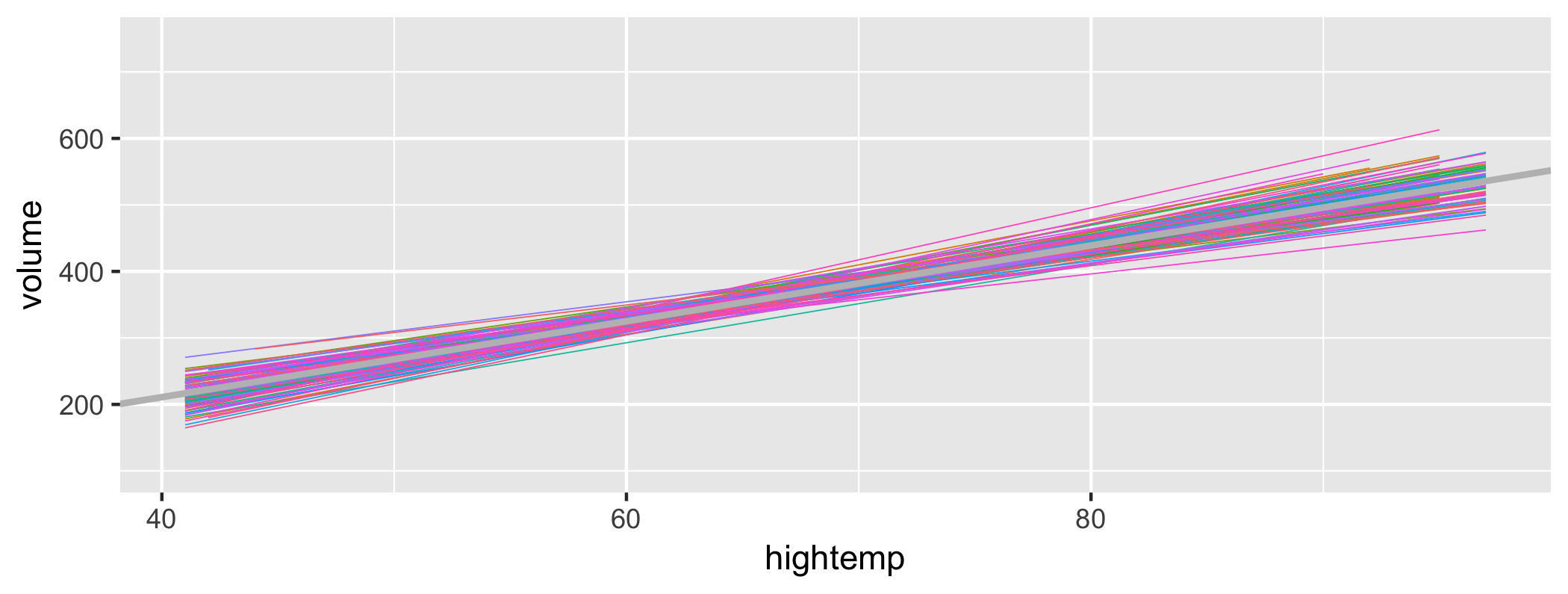<!-- --> --- ## Bootstrap interval for the slope .small[ <div class="question"> 👤 Interpret the 95% confidence interval for the slope of the regression line for predicting volume (estimated number of trail users that day) from hightemp (daily high temperature, in F). </div> ] .small[ .pull-left[ ```r boot_dist <- RailTrail %>% specify(volume ~ hightemp) %>% # generate(reps = 100, type = "bootstrap") %>% calculate(stat = "slope") ``` ] .pull-right[ ```r boot_dist %>% summarise(l = quantile(stat, 0.025), u = quantile(stat, 0.975)) ``` ``` ## # A tibble: 1 x 2 ## l u ## <dbl> <dbl> ## 1 4.077062 7.529332 ``` ] ] 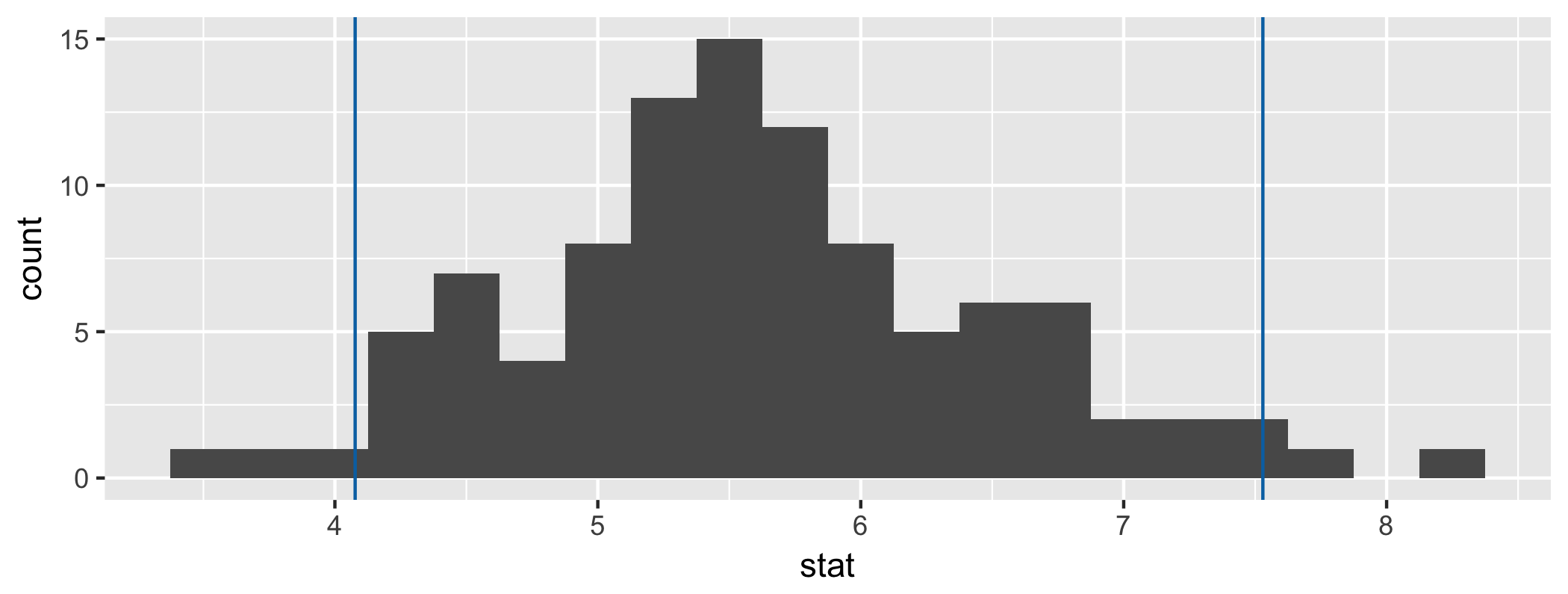<!-- --> --- ## Hypothesis testing for the slope `\(H_0\)`: No relationship, `\(\beta_1 = 0\)` **vs** `\(H_A\)`: There is a relationship, `\(\beta_1 \ne 0\)` <div class="question"> 👥 What is the conclusion of the hypothesis test? </div> .small[ ```r null_dist <- RailTrail %>% specify(volume ~ hightemp) %>% hypothesize(null = "independence") %>% generate(reps = 100, type = "permute") %>% calculate(stat = "slope") ``` ] 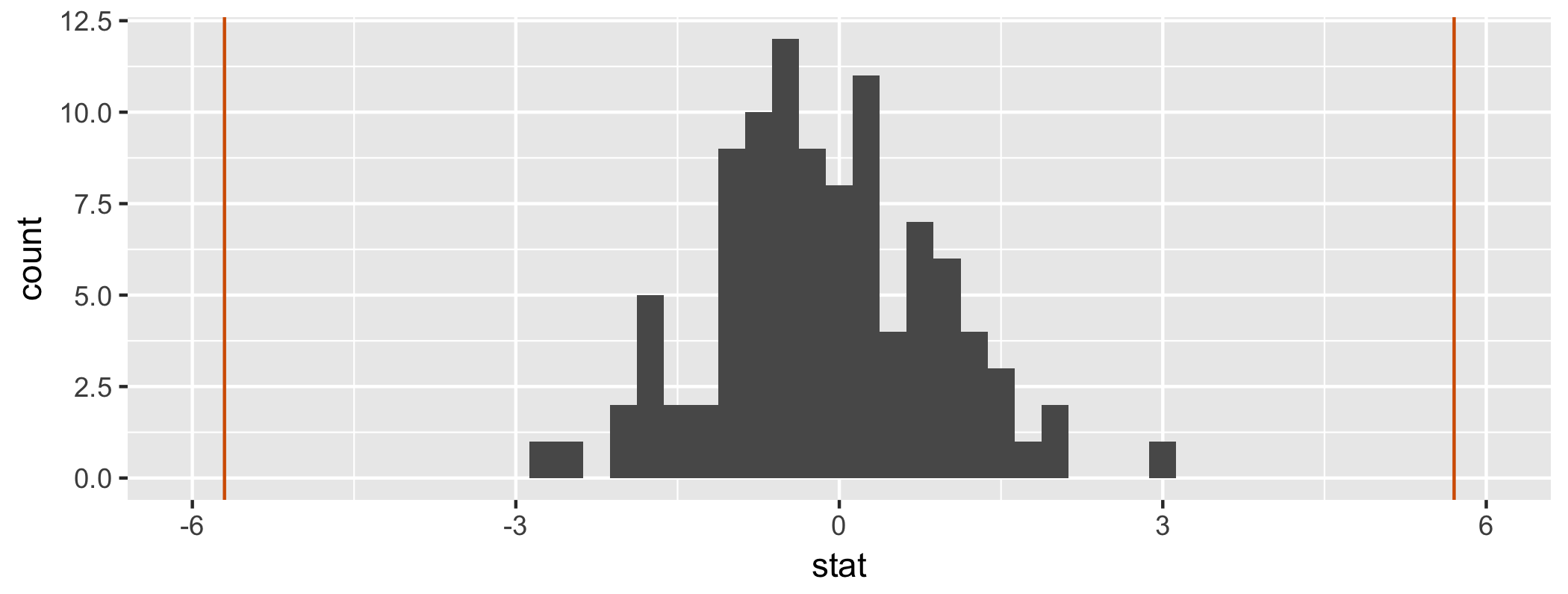<!-- --> --- ## Finding the p-value ```r null_dist %>% filter(stat >= m_riders$coefficients[2]) %>% summarise(p_val = 2 * n()/nrow(null_dist)) ``` ``` ## # A tibble: 1 x 1 ## p_val ## <dbl> ## 1 0 ``` --- class: center, middle # Sample Statistics and Sampling Distributions --- ## Notation - Means: - Population: mean = `\(\mu\)`, standard deviation = `\(\sigma\)` - Sample: mean = `\(\bar{x}\)`, standard deviation = `\(s\)` - Proportions: - Population: `\(p\)` - Sample: `\(\hat{p}\)` <br/> - Standard error: `\(SE\)` --- ## Variability of sample statistics - Each sample from the population yields a slightly different sample statistic (sample mean, sample proportion, etc.) - The variability of these sample statistics is measured by the **standard error** - Previously we quantified this value via simulation - Today we talk about the theory underlying **sampling distributions** --- ## Sampling distribution - **Sampling distribution** is the distribution of sample statistics of random samples of size `\(n\)` taken with replacement from a population - In practice it is impossible to construct sampling distributions since it would require having access to the entire population - Today for demonstration purposes we will assume we have access to the population data, and construct sampling distributions, and examine their shapes, centers, and spreads <div class="question"> What is the difference between the sampling and bootstrap distribution? </div> --- class: center, middle # Central Limit Theorem --- ## In practice... We can't directly know what the sampling distributions looks like, because we only draw a single sample. - The whole point of statistical inference is to deal with this issue: observe only one sample, try to make inference about the entire population - We have already seen that there are simulation based methods that help us derive the sampling distributiom - Additionally, there are theoretical results (**Central Limit Theorem**) that tell us what the sampling distribution should look like (for certain sample statistics) --- ## Central Limit Theorem If certain conditions are met (more on this in a bit), the sampling distribution of the sample statistic will be nearly normally distributed with mean equal to the population parameter and standard error proportional to the inverse of the square root of the sample size. - **Single mean:** `\(\bar{x} \sim N\left(mean = \mu, sd = \frac{\sigma}{\sqrt{n}}\right)\)` - **Difference between two means:** `\((\bar{x}_1 - \bar{x}_2) \sim N\left(mean = (\mu_1 - \mu_2), sd = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} \right)\)` - **Single proportion:** `\(\hat{p} \sim N\left(mean = p, sd = \sqrt{\frac{p (1-p)}{n}} \right)\)` - **Difference between two proportions:** `\((\hat{p}_1 - \hat{p}_2) \sim N\left(mean = (p_1 - p_2), sd = \sqrt{\frac{p_1 (1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}} \right)\)` --- ## Conditions: - **Independence:** The sampled observations must be independent. This is difficult to check, but the following are useful guidelines: - the sample must be random - if sampling without replacement, sample size must be less than 10% of the population size - **Sample size / distribution:** - numerical data: The more skewed the sample (and hence the population) distribution, the larger samples we need. Usually n > 30 is considered a large enough sample for population distributions that are not extremely skewed. - categorical data: At least 10 successes and 10 failures. - If comparing two populations, the groups must be independent of each other, and all conditions should be checked for both groups. --- ## Standard Error The standard error is the *standard deviation* of the *sampling distribution*. - **Single mean:** `\(SE = \frac{\sigma}{\sqrt{n}}\)` - **Difference between two means:** `\(SE = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}\)` - **Single proportion:** `\(SE = \sqrt{\frac{p (1-p)}{n}}\)` - **Difference between two proportions:** `\(SE = \sqrt{\frac{p_1 (1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}\)`