Binomial Probabilities
Let's look at the binomial random variable with n=10 and p=.3 or Bin(10, .3). In Matlab, to find P(y=3), type
>> binopdf(3, 10, .3)Does it agree with
>> nchoosek(10,3)*0.3^3*(1-0.3)^7where the command "nchoosek" returns the binomial coefficient
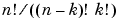 .
. To find P(y <=3) which is the cumulative distribution function evaluated at 3, type
>> binocdf(3, 10, .3)Does it agree with
>> sum(binopdf(0:3, 10, .3))Try the following two commands and explain the results.
>> binocdf(3.5, 10, .3) >> binopdf(3.5, 10, .3)Find the mean and variance of Binomial random variable with n=10 and p=0.3, and compute P(mean - sd < y < mean + sd) where "sd" stands for "standard deviation".
[mean,var] = binostat(10,.3); sd = sqrt(var); mean + sd mean -sd binocdf(mean + sd, 10, .3) - binocdf(mean - sd, 10, .3)Compare the result with the Empirical Rule. If "mean + sd" happens to be an integer, will the commands above give you the right answer? (the answer is NO.) What kind of adjustments you need to do?
Next let's draw Binomial probability distributions for n =10 and p = 0.3, 0.5, 0.7. We will draw them in the same Figure window. Note the symmetry of the distribution for p=0.5 and the skewness for p=.3 and p=.7.
clf % erase the contents of a Figure window without closing it.
y = binopdf(0:10, 10, 0.3);
subplot(2,2,1); % subdivide the current Figure window into a 2-by-2
% array of plotting area and chooses the 1st area to
% be active.
stem(0:10, y);
legend('Bino n=10, p=0.3')
y = binopdf(0:10, 10, 0.5);
subplot(2,2,2); % choose the 2nd area to be active.
stem(0:10, y);
legend('Bino n=10, p=0.5')
Write your commands for plotting the Binomial probability distribution
with p=0.7 in the 3rd plotting area.Draw the cumulative distribution function for Bin(10, .3)
x=0:10;
y = binocdf(x, 10, 0.3);
stairs(x, y);
legend('Cumulative Distribution Function for Bin(10, .3)', 4);
Geometric Distribution
Warning: Matlab uses geometric(p) to refer to
the distribution of the number of trials before the first success,
which corresponds to the distribution of "y - 1", with y as defined in our
textbook.
Let's draw Geometric probability distributions for p=0.3 and p=0.7.
y1 = geopdf(0:9, 0.3);
y2 = geopdf(0:9, 0.7);
h1 = stem(1:10, y1, 'o');
% h = stem(...) returns handles to three line graphics objects:
% h(1) - the marker symbol at the top of each stem
% h(2) - the stem line
% h(3) - the base line
hold on; % add new plot to the existing axes
h2 = stem(1:10, y2, 'x');
set(gca, 'XLim', [0.5 10.5]);
legend([h1(1),h2(1)], {'p=0.3','p=0.7'})
title('Geometric Probability Distributions');
hold off; % release the current Figure window for new plots
Summary of Commands for Discrete Distributions
Today we learned three kinds of Matlab commands related with discrete distributions. They are commands for Probability Density Functions (ending with pdf), for Cumulative Distribution Functions (ending with cdf) and for Mean and Variance (ending with stat). The corresponding commands for each distribution are listed below:
binopdf, binocdf, binostat
geopdf, geocdf, geostat
hygepdf, hygecdf, hygestat
nbincdf, nbinpdf, nbinstat