Bootstrap Confidence Intervals¶

We present a problem and show a model based approach to estimating confidence intervals then we follow up with a bootstrap based approach. This example implements the bias-corrected and accelerated $BC_{a}$ method to calculate confidence intervals. The notation us borrowed from Efron and Tibshirani’s An Introduction to the Bootstrap [1].

The Problem¶

Ten university students were recruited to play the seminal video game pac-man. After equal amounts of practice the students were then asked to play the first stage and the time to completion was recorded. The following data in seconds were recorded.

>>> import numpy as np
>>> x = np.array([63.1,64.6,63.4,65.6,63.4,65.7,64.6,63.1,65.9,63.3])

Method 1¶

Because we do not know the population variance the sample standard deviation 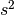$s^{2}$ can be used as a subsitute.

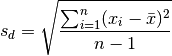
$\begin{equation*} s_{d} = \sqrt{\frac{\sum^{n}_{i=1} (x_{i} - \bar{x} )^{2}}{n-1}} \end{equation*}$

>>> sd = np.sqrt(np.sum(np.power(x - x.mean(),2)) / (x.size-1))
>>> sd
1.1489608831945115

Then we can calculate the CI as

$\begin{equation*} CI: \left(\bar{x} \pm t_{n-1},1-\frac{\alpha}{2} \times \frac{s_{d}}{\sqrt{n}} \right) \end{equation*}$

>>> import scipy.stats as stats
>>> alpha = 0.05
>>> interval = stats.t.ppf(1.0 - (alpha / 2.0),x.size-1) * (sd / np.sqrt(x.size))
>>> ci = (x.mean() - interval, x.mean() + interval)
>>> ci
(63.448082897537432, 65.09191710246256)

We are 95% confident that the true population mean lies between 63.45 and 65.09.

Method 2¶

let $\mathbf{x}^{*}$ be a nonparametric bootstrap sample from the empirical distribution $\hat{F}$

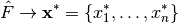
$\begin{equation*} \hat{F} \rightarrow \mathbf{x}^{*} = \{ x_{1}^{*}, \ldots, x_{n}^{*} \} \end{equation*}$

We note that the difference among the means hints that the treatment group may have longer survival times in general.

Example from immunology¶

In these data we have reason to believe that the confidence intervals will not always be symmetric about $\hat{\theta}$ . We use two methods to illustrate the differences in CI estimates. Let the data be the cytokine responses (%) for a sample measured by 16 laboratories. For the purposes of this example we will assume independence among the samples.

>>> import numpy as np
>>> x = np.array([0.4043, 0.5958, 0.5876, 0.5939, 0.6053, 0.4649, 0.5722,\
... 0.6234, 0.5208, 0.6117, 0.6137, 0.7397, 0.6981, 0.7757, 0.7596, 0.532])

Method 2 - The $BC_{a}$ method described above

Further Notes¶

An alternative way to analyze these data is to use normal theory and assume that both underlying distributions are Gaussian. We can then calculate the achieved significance level ASL as

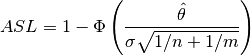
$ASL = 1 - \Phi \left( \frac{\hat{\theta}}{\sigma \sqrt{1/n+1/m}} \right)$

where 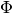$\Phi$ is the standard normal cdf. Because $\sigma$ is unknown we can use

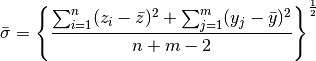
$\bar{\sigma} = \left\{ \frac{ \sum^{n}_{i=1} (z_{i}-\bar{z})^{2} + \sum^{m}_{j=1} (y_{j}-\bar{y})^{2} } {n+m-2} \right\}^{\frac{1}{2}}$

>>> sigma_bar = np.sqrt((  np.sum((z-z.mean())**2) + np.sum((y-y.mean())**2) ) / (z.size + y.size - 2.0))
>>> sigma_bar
54.235210425392665

such that

>>> import scipy.stats as stats
>>> 1.0 - stats.norm.cdf(theta_hat / (sigma_bar * np.sqrt((1.0/z.size)+(1.0/y.size))))
0.13117683784495782

Instead of estimating the variance with $\bar{\sigma}$ , a fixed constant, we can use Student’s t-test.

>>> 1.0 - stats.t.cdf(theta_hat / (sigma_bar * np.sqrt((1.0/z.size)+(1.0/y.size))),14)
0.1406062923976501

In both cases we fail to reject the null.

Literate Programming

Bibliographic notes¶

Efron, Bradley and Tibshirani, R. J., An Introduction to the Bootstrap,Chapman & Hall/CRC Monographs on Statistics & Applied Probability, 1994.