- Create boxplots of the lifetimes in each group. Use Display 3.5 to comment on the possible implications of using a pooled standard deviation in this case.
- Use the Welch t-tools to find a 2-sided p-value and confidence interval for the effect of treatment on the lifetimes of guinea pigs. Express your result in a sentence. In Splus, go to the two-sample t-test menu and click the box next to "unequal variances."
- Comment on the adequacy of an "additive treatment model" for these data. That is, how well can these data answer the question of whether the bacilli treatment appears to cause an additive change in the mean of the lifetimes?
The eating habits of 20 bats were examined in the article "Foraging Behavior of the Indian False Vampire Bat" (Biotropica (1991):63-67). These bats consume insects and frogs. During the course of the study, 8 of the bats contracted a virus, and thus, data were only available for a sample size of 12 bats. For the 12 bats, the sample average time to consume a frog was 21.9 minutes. The sample standard deviation was 7.7 minutes. Two analysts considered the data, and constructed 99% confidence intervals for the mean suppertime of a vampire bat whose meal consists of a frog.
- Analyst 1 used the 12 observations to construct her confidence interval. Report her result and interpret it in a sentence.
- Analyst 2, knowing that it's
always better to have a larger sample size, decided to fill in the
missing data using the sample mean. (This is a very naive method of
data imputation.) She assumed that her sample
size was 20, and filled in each of the 8 missing observations with
the value of the sample average, 21.9 minutes. She then calculated
her 99% confidence interval. Clearly write out the following
quantities that Analyst 2 used to form the confidence interval:
,
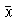n, s, and the value of
t-quantile. Report the confidence interval and compare it to
your result in part (a). If you were reviewing Analyst 2's work for
a journal, would you accept it? Why or why not? Note: to calculate
s for Analyst 2, you may
need to refer to the formula for s on
page 20 of the Sleuth.
- Both Analyst 1 and Analyst 2 use their 99%
confidence intervals to determine whether there is evidence that the mean suppertime of a vampire bat differs from 20 minutes. Write out the hypotheses considered. Is one more likely than the other to reject the null hypothesis? Why or why not?
Sleuth #3.24 on page 79. Sex Discrimination data. Turn in answers to (b) and (c) only.
Some Directions:
- In (a), create boxplots and QQ-normal plots of both the untransformed and transformed data to determine whether the log transform is appropriate. You don't have to turn this in.
In Splus, log transform the data by creating a new column in Splus. Do this by going to "Data" and "Transform". Give your new variable a name in "Target Column". I'll refer to it as "log.sal". In the box next to "Expression", type "log(salary)". A new column is created in your dataframe. Once you have transformed the data, calculate and print out summary statistics for log transformed data by group. Use these in (b).
-
It happens for this data that the analysis could be done on either the original scale or the log transformed scale (Do you agree? Make some histograms and QQ plots and see). For the purpose of giving you some practice with calculations and interpretations after log transforms, though, perform your analysis on the log scale.
Splus Directions for a "QQ-Normal" plot: Go to "Graph" and "2D Plots" and "QQ Normal with Line (y)". Under ``y columns'' type the name of the variable you want to plot. If you want to make a QQ-Normal plot for only the "code=1" group, in the QQ Plot Menu, go to "Subset Rows with" and enter "code==1". This will limit the plot only to those measurements with code=1. Make sure you enter 2 "="'s.
In (b), give hypotheses and test statistic, show how you arrived at the p-value, and write a 1-sentence conclusion. This can be handwritten. Show all steps.
In (c) give the confidence interval and a sentence. Show all steps.
Sleuth #3.31, p. 79. Brain/litter size
This is another 1 page (max) data analysis write-up. Refer to HW2 for guidelines on writing this up. Please put your answer to this problem on a separate page, with your name on it.
Some points to cover for this example:
Exploratory Analysis of Data section: Again, a single figure as well as summary statistics should be enough here. For the figure, you can create a boxplot of the data on the natural scale (the log scale isn't intuitive for most people). In describing a dataset that has some skew, your summary statistics should include resistant measures of center and spread of the distribution. If there is an unusually large or small observation, you should note it.
Statistical Analysis section: Here you should consider a transformation of the data. You do not need to describe every transformation you tried, just give the results for your final choice. You should describe briefly the motivation behind any transformations you might have chosen. Evaluate whether the transformation is appropriate by boxplotting transformed and untransformed data, as well as creating QQ-normal plots of transformed and untransformed data. You won't put all of these plots in your writeup, but you can describe the properties of your transformed data. Then you should perform a comparison of the two groups and give a p-value for your results. "Appropriate measures of uncertainty" means a confidence interval. Take some care in interpreting your tests and intervals if you have transformed your data. If your dataset includes outliers, you should run your tests with and without the points of concern to see if your results differ.
Scope of Inference section: If you have transformed your data in order to fit the model, be sure your interpretations are expressed on the original scale of measurement or some scale meaningful to your reader. If you had to make assumptions to perform your statistical tests (like normality of transformed populations and independence of samples), think about whether these assumptions were realistic given the data that you have, and whether you really can answer the research question at hand. Give information on the extent to which the findings can be generalized to populations and whether a causal relationship can be established.