To turn in:

1. As part of the Free Air CO₂ enrichment study, a set of experiments are conducted in Duke Forest to determine whether plants grown under elevated atmospheric CO₂ (this is the future climate scenario for CO₂ in 2050) can more effectively photosynthesize carbon. Some loblolly pine trees are exposed to a 50% increase in ambient atmospheric carbon dioxide (CO₂ ) as compared to control trees. Since carbon and nitrogen cycles are closely linked, researchers measure leaf nitrogen (N) content, in % of N in a leaf per total leaf mass. (The leaves are actually pine needles from the loblolly pines.) The Duke scientists want to design an experiment to find out whether atmospheric CO₂ affects leaf N in loblolly pine trees.

   Preliminary measurements produce the following data:

   Treatment: 1.121, 1.29, 1.183, 1.145, 1.168, 1.316, 0.998, 1.174

   Control: 1.012, 1.111, 1.014, 1.091, 1.098, 1.179

   1. The researchers use the preliminary data above to get an estimate of s_pooled. They then design a study to test whether leaf N levels increase with increased CO₂ levels. They set a Type I error rate of 5%, and plan for 5 trees in each group. Calculate the power of this test to detect an increase in leaf N levels of 0.05 for the treatment group over the control group.

      To calculate the power, first use the data above to find s_pooled and then calculate the rejection region under H_ousing n=5/group for the proposed two-sample test. Re-express the rejection region for the test in terms of the difference in sample means. Then see what that rejection region means in terms of the alternative hypothesis.

   2. Using the approximate sample size formula given in class, calculate the required sample size to achieve 95% power for a=.05 and a difference in means of 0.06.

   3. Again using the approximate formula, what difference in means can be detected under the following conditions: total of 10 trees studied (5/group), 5% Type I error and 5% Type II error. How does this answer compare to your answer in (a)?

   4. Make a plot of power curves using the script file power.curve.S. Consider a range of sample sizes for each group (n=5, 10, 15, 20, 50), and a range of treatment effects between 0.02 and 0.2. What levels of power can be achieved at each sample size when a difference in means of 0.08 is desired? (Read these off graph.)

      To run this function, you will need to provide 4 arguments exactly in this format:

      For s=33,alpha=.05, samples sizes of n=5, n=10, n=40, n=80, and a range in treatment effects of 2 to 22, type the following in the command window (after loading the script file):
      power.curve(33,.05,c(5,10,40,80),c(2,22))

   5. Repeat the exercise above, increasing s_pooled by 50%. Describe the differences in the two plots.

   6. The Duke researchers have budgeted for tests to be run on 5 trees in each group. In a few sentences, use the graphs to explain to them why it might be beneficial to increase the sample size and minimize measurement error in their samples. (They took Sta240 many years ago and remember nothing about power and errors in statistical tests.)

2. In a statement before Air and Water Pollution Subcommittee of the Senate Public Works Committee on June 26, 1973, Mr. John McKinley, President of Texaco, cited an automobile filter developed by Associated Octel Company as effective in reducing pollution. However, questions had been raised about the effects of Octel filters on vehicle performance, fuel consumption, exhaust gas back pressure, and silencing. Let's say that young congressional aide Ralph Nader is pushing for a new study of these filters, since he is sure that the auto industry is engaging in a conspiracy to delay development and use of air pollution control devices. He wants to make sure that the Octel filter does not produce higher noise levels than the standard filter. A study is planned in which noise level readings (in decibels) are compared between the Octel filter and standard filters.

   We will evaluate the power of a hypothesis test in which the claim is that the mean noise level of the Octel filter is lower than the mean noise of the standard filter. Let X be the noise measurement for a car with a standard filter, and Y be the noise measurement for a car with the Octel filter. Based on an analysis of 72 cars (36 cars fitted with a standard filter and 36 cars fitted with the Octel filter) it is assumed that is equal to 27.4.

   1. Write out the null and alternative hypotheses for such a hypothesis test.

   2. For what values of 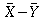will we fail to reject the null hypothesis? Let 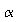= 0.05.

   3. Evaluate the power of the test to detect a reduction of 5 decibels in the noise level of the Octel filter versus the standard filter. That is, you will evaluate the power of the test when 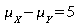. Do this calculation by hand, then verify that you are in the ballpark using Splus. (In the dialogue box for power "test type" will be "greater than".)

      For the sample size problems below, follow these Splus directions.

   4. Give the required sample size needed in order to detect at least a 5 decibel noise reduction by the Octel filter over the standard filter with 80% power. Use 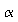= 0.05. (Note that in Splus, you'll need to specify the test type as "greater than" .)

   5. Give the required sample size needed in order to detect at least a 5 decibel noise reduction by the Octel filter over the standard filter with 80% power. Use 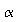= 0.01.

   6. Give the required sample size needed in order to detect at least a 5 decibel noise reduction by the Octel filter over the standard filter with 80% power. Use 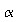= 0.05, but this time assume that 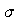=15.

3. Read the paper by Ripple, et al. on E-reserve, as well as the papers on sampling issues by Marks et al. Note that Ripple et al. located 30 nest sites, and then obtained 30 randomly selected locations that were assumed not to be nest sites. The data are here, and are also described in Exc. 15 on page 605 of Sleuth. Note that the data are percentages, and that you will want to transform them into proportions.

   The research question is: Is the percentage of mature forest larger at nest sites than at random sites? How much larger? Give (and explain) an appropriate measure of uncertainty (a CI).

   You will analyze results for the outer radii of 2.41 km and 3.38 km. Use our class format for a 1-page writeup, not the format of Ripple. The paper is intended to give you some background on data collection and give you an example of a statistical analysis that (I think you'll agree) is in need of improvement.

   Be sure to make boxplots/qqplots of the data for each case, on the untransformed scale, the log scale, the arcsin square root scale, and the logit scale, and decide which is most appropriate. Remember, we want to be able to interpret the results on the original scale.

   Note: To do the arcsin square root transformation, you'll need to type the following (using pctring6 as an example): "asin(sqrt(pctring6/100))"

   ---

   Some general questions to think about as you read the article and evaluate the quality of the statistical analysis they did (you do not need to include the answers to these in your report unless they are relevant to our method of writing one page summaries).

   1. Why do you think that the authors chose the arcsin transformation? What other transformation might have been appropriate?

   2. What assumptions were necessary for the test used? On what scale are these assumptions made?

   3. Give one possible way that the independence assumption could have been violated.

   4. Why should the authors include a more resistant set of summary statistics than those given in Table 1? What statistics should be included? What plot(s) would you include?

   5. Practice problem: One of the circular plot sizes chosen for the study was 1826 ha, or about a 1.5 mile radius. For this plot size, in statistical notation, give the authors' hypotheses, degrees of freedom for the test statistic, and conclusion of the test. Is the p-value they report one-sided or two-sided?

   ---