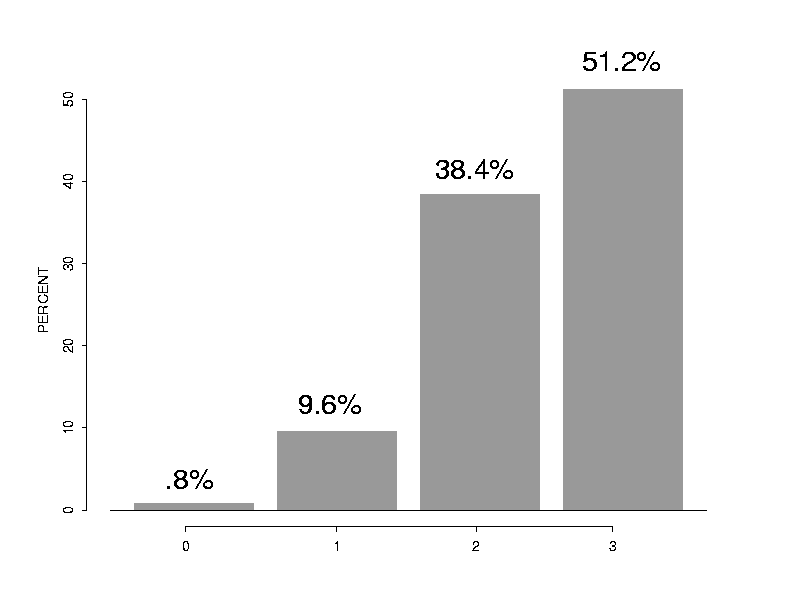
4-4 (p. 112)
a. 

x   p(x)
0   0.008
1   0.096
2   0.384
3   0.512

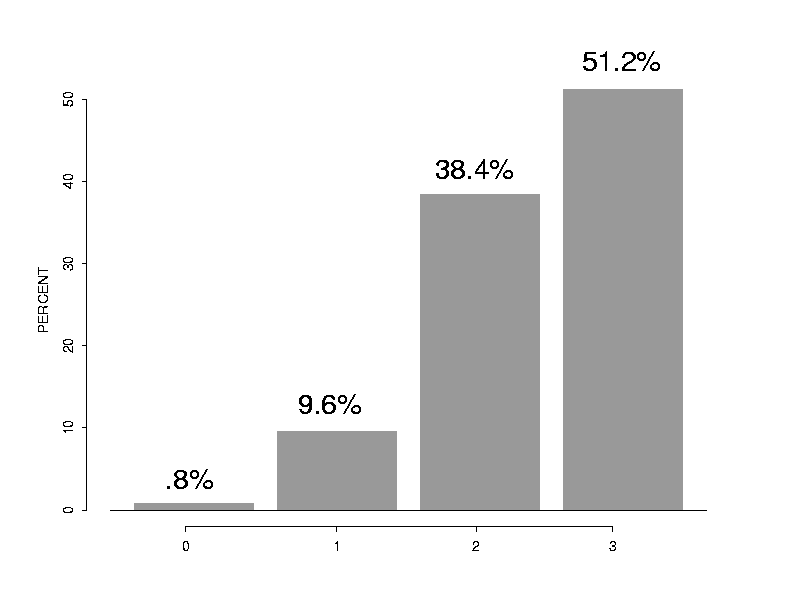
b. P(at least 2 sales) = P(2 sales) + P(3 sales) = 0.384 + 0.512 = 0.896

4-8 (p. 115)
a.expected (mean) attendance: ($5000)(0.20) + ($20000)(0.20) + ($30000)(0.10) + ($50000)(0.50) = 33000
b.X:number in attendance
Y:profit
Y = ($9)X - ($2)X - $150000 - $60000 = 7X - 210000
expected profit = mean of Y:
($7)(33000) - $210000 = $21000
Taking into account what will be made and what will be spent, the expected profit is $21000. However, the probability is only 50% that he'll make money.

4-12 (p. 122)
a.n=100, pi=0.5, average(mean) of S=50
b.n=30, pi=1/6, average(mean) of S=5
c.n=20, pi=0.5, average(mean) of S=10
d.mean for any binomial variable: n(pi)

4-14 (p. 123)
a.n=12, pi=0.2
P(8 or more of 12) = P(8 of 12) + P(9 of 12) + P(10 of 12) + P(11 of 12) + P(12 of 12) = 0.00058 (approx)
b.n=12, pi=0.5
P(8 or more of 12) = P(8 of 12) + P(9 of 12) + P(10 of 12) + P(11 of 12) + P(12 of 12) = 0.19385 (approx)
c.n=10, pi=0.2
P(6 or more of 10) = P(6 of 10) + P(7 of 10) + P(8 of 10) + P(9 of 10) + P(10 of 10) = 0.00637 (approx)

4-22 (p.134)
mean=110 minutes, sd=20 minutes
a.P(X <= 120) = P(Z <= (120-110)/20) = P(Z <= 0.5) = 1 - P(Z > 0.5) = 1 - 0.309 = 0.691
b.P(X <= x) = 0.90
P(Z <= (x-110)/20) = 0.90
(x-110)/20 = 1.28
x = (1.28)(20) + 110
x = 135.6 minutes

4-26 (p. 140)
X = number of contracts he gets
Y = profit
a.Expected number of contracts he gets: n(pi) = (0.40)(6) = 2.4 (see problem 4-12)
b.Y = $200X - $300
Expected profit: E(Y) = $200(2.4) - $300 = $180
c.He will only make money (get "positive profit") if he gets 2 or more contracts. He will lose money ("negative profit") only if gets fewer than 2 contracts.
P(lose money) = P(X <= 1) = P(X=0) + P(X=1) = (0.6)^6 + 6(0.4)(0.6)^5 = 0.23328
P(make profit) = P(X > 1) = 1 - P(X <= 1) = 1-0.23328 = 0.76672