Sta 242 / Env 255

Homework 4

Problem #2 due Tuesday, February 13, at class

Problem #3 due Thursday, February 15, at class



  1. Rainfall and corn yield.Problem 15 of Chapter 9. This problem will not be turned in, but is suggested.

    Data in EX0915.ASC.

    What you should learn from this problem: In (b), you should be able to test whether the addition of a quadratic term explains a significant amount of the variation in corn yield. You should understand what the motivation for plot (c) is, and what it tells you. In (d), you should begin to see the dynamics of how estimates of parameters, their standard errors, and model error change as additional parameters are added to the model. You should know how to interpret the meaning of a single coefficient in the context of a multiple regression model. And you should understand if rescaling the year variable changes or doesn't change interpretations of a model. You should understand how the year variable fits into the model. In (e), you should be able to write out a formal test for the significance of the interaction effect and explain the interaction effect in terms of the effect of rainfall on yield for different time periods.

    Additional instructions:

    In (a) use a regression line plot to evaluate graphically the fit of the simple linear model.

    In (d), note there are 5 subquestions asked. Here is part (vi): In part (d) you will add year to the model. Refit the regression line by rescaling year: use "Data" - "Transform" to create a new variable, year - 1890 . Which of the two regression lines (with year as it is given or with year rescaled) would you prefer and why?

    Splus instructions:

    1. For part (c), run the regression yield~rainfall+rainfall^2 . In the "Results" tab, check the box for "Residuals" and choose to "Save In:" the existing dataset, EX0915.ASC. Then use this residual column for your plot.

    2. For part (e), your model formula is: yield~rainfall+rainfall^2+year+year:rainfall Note the format for an interaction term.




  2. Pollen Removal: problem 16(c)-(e) on page 252 of Sleuth. Problem 16 (a) and (b) are suggested, but not to turn in.

    Data in pollen.txt. Variables: "removed", "duration", "code" (0=queens; 1=workers).

    Data is shown on page 77 of Sleuth. An additional brief description of the data is given at the bottom of page 75 of Sleuth, #26.

    What you should learn from this problem: Familiarity with a logit transformation and its meaning in terms of odds that pollen is removed; interpreting the meaning of coefficients in this type of model. Walking through consideration of three types of models: single line, parallel lines, and non-parallel lines. Knowledge of how to plot these models will be useful to your projects. Understanding dynamics of how p-values change with addition/deletion of variables. Often a categorical variable (such as queen/worker status) can be a "lurking" variable in a regression problem; ignoring it can be misleading. Many regressions you will see this semester will contain both categorical and continuous variables. Finally, the ESS F-test will be a focus of model selection for the rest of the semester.

    Additional instructions:

    1. Put all graphs on separate pages at the end of the homework.

    2. In (c), create a regression line plot for the model of logit(fraction removed)~log(duration) (ignoring queen/worker status). This is the "equal lines" model in Display 9.8. Remember that you can enter "CODE" as your z-variable. Suggested but not to turn in: plot residuals vs. fitted for this model.

    3. In (d), plot the multiple regression model you have fit (it will be one of the types of models shown in Display 9.8, p. 239). This will require the command line in Splus (see Splus instructions below). Suggested but not to turn in: plot residuals vs. fitted for this model and look for violations of assumptions.

    4. In (e), note there are 3 subquestions. Number each (i) through (iii). Here is part (iv): plot the multiple regression model you have fit (it will be one of the types of models shown in Display 9.8, p. 239). This will require the command line in Splus (see Splus instructions below). Suggested but not to turn in: plot residuals vs. fitted for this model and look for violations of assumptions.

    5. Additional Part (f). Use the model you fit in (e) to write a sentence on the effect of a doubling in duration on the odds that pollen is removed for workers.

    6. Additional Part (g). This exercise introduces material in Section 10.3, the Extra Sum of Squares F-test (Display 10.12 is particularly helpful here). We wish to test the following hypotheses in order to assess the significance of a queen/worker effect in the linear model relating the odds that pollen is removed to the duration of visit. The variable "code" below refers to the indicator variable for queen/worker status.

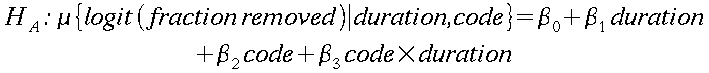
      Perform an extra Sum of Squares F-test and state your conclusion in a sentence. Here you are evaluating whether adding terms for queen/worker status as well as an interaction term between queen/worker status and duration significantly improves the predition of the mean log odds that pollen is removed.

    Splus instructions:

    1. To produce a coded scatterplot in (a), refer to the Splus hints from Homework 3.

    2. For part (b) you'll need to create a new variable, log[p/(1-p)], by going to "Data" - "Transform" and typing in the formula: log((removed)/(1-removed)) .

    3. To produce the additional plots mentioned for (d) and (e), you will need to use the command line.

      First, go to the command line and check what is in your directory by typing, "ls()". This will list the objects in your directory.

      The following commands will produce a plot for a dataset called "pollen.txt", where the transformed columns are named "logit.frac", "log.dur", "code". Let "log.dur" and "logit.frac" be continuous variables and let "code" be an indicator variable. We assume that "code" is coded as a "0" or a "1". The first command, "attach", allows you to refer to the variable names in the dataframe directly. Without it, Splus command line only knows about "pollen.txt" but not the names of the variables in it.

      attach(pollen.txt)

      plot(log.dur,logit.frac,type="n",xlab="Log(Duration)",ylab="Logit(fraction removed)")

      points(log.dur[code==0],logit.frac[code==0],pch="Q")

      points(log.dur[code==1],logit.frac[code==1],pch="W")

      title("Whatever title you want")

      Now you want to plot the regression lines for each level of the indicator variable. First, you'll need to calculate the slope and intercept of the lines you will add. To add a line to your plot, use the command "abline(intercept,slope)". So let's add a line to our plot with intercept 1.5 and slope 2.

      abline(1.5,2)

      You can add each line in a similar way.

      Getting Fancy: You can make a dotted line by adding "lty=2" to the abline command, so that it reads abline(1.5,2,lty=2).




  3. Ecosystem Decay. Problem #21, Chapter 8, page 222 of Sleuth. Data in EX0821.ASC.

    As in Homework 2, you are to produce a formal 1-page report.

    What you should learn from this problem: As before, this is practice for the take-home midterm.

    Refer to Homework 2 for guidelines in producing this report. You can also refer to the solutions for Homework 2 which give examples of good data analysis reports. (Reminders: they are to be typed, with no raw Splus output, 1-page maximum, organized, concise.)

    Some points to cover for this example: