Sta 242 / Env 255

Homework 2

Due Thursday, February 14 in class

  1. Fisk and Sammarco found that the skeletal density of the coral Porites lobata increases with distance from the Australian shore due to differences between inshore and offshore environments. The dataset, reef.txt, provides the following data for the density of Great Barrier Reef coral heads:

    1. Produce a regression line plot of Y=coral head density vs. X=distance to shore.

    2. Report the fitted regression line. In one sentence each, interpret the slope, intercept and R2. (Look under "Example - Big Bang" on p. 173 for an example of such interpretations, and also refer to HW1 solutions for the format/syntax here.)

    3. Assess lack of fit of the linear regression model by a plot of residuals vs. fitted values.

    4. Assess lack of fit of the linear regression model using the lack of fit F-test.

    5. Investigating a polynomial fit. We will now consider the following regression model:

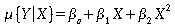
      1. First, make a plot of this fitted model for the coral reef data. Go to "Graph" - "2D Plot" - "Fit-Polynomial Curvefit". Choose the X and Y variables as before. Click on the "Curve Fitting" tab and check that you are fitting "Curve Fit Type: Linear" and "Poly. Order 2". Click "OK" to produce the plot.
      2. Next, fit the model by choosing "Statistics" - "Regression" - "Linear". In the "Formula" box, type "Density~Distance+Distance^2". Write out the fitted model.
      3. In the regression output for the fitted model, look at the p-value corresponding to "I(Distance^2)". This is the p-value for the two-sided hypothesis test of Ho: b2 = 0 in the presence of b0 and b1. That is, we are comparing the simple linear model to the polynomial model of degree 2. What does the p-value say about the polynomial model?

  2. Butterfly ballots in Palm Beach County, Florida. The U.S. presidential election of November 7, 2000 was one of the closest in history. As returns were counted on election night it became clear that the outcome in the state of Florida would determine the next president. At one point in the evening, television networks projected that the state was carried by the Democratic nominee, Al Gore, but a retraction of the projection followed a few hours later. Then, early in the morning of November 8, the networks projected that the Republican nominee, George W. Bush, had carried Florida and won the presidency. Gore called Bush to concede. While on route to his concession speech, though, the Florida count changed rapidly in his favor. The networks once again reversed their projection, and Gore called Bush to retract his concession. When the roughly six million Florida votes had been counted, Bush was shown to be leading by only 1,738, and the narrow margin triggered an automatic recount. The recount, completed in the evening of November 9, showed Bush's lead to be less than 500.

    Meanwhile, angry Democratic voters in Palm Beach County complained that a confusing "butterfly" lay-out ballot (see here for a picture) caused them to accidentally vote for the Reform Party candidate Pat Buchanan instead of Gore. The ballot listed presidential candidates on both a left-hand and a right-hand page. Voters were to register their vote by punching the circle corresponding to their choice, from the column of circles between the pages. It was suspected that since Bush's name was listed first on the left-hand page, Bush voters likely selected the first circle. Since Gore's name was listed second on the left-hand side, many voters who already knew who they wished to vote for did not bother examining the right-hand side and consequently selected the second circle in the column; the one actually corresponding to Buchanan. Two pieces of evidence supported this claim: Buchanan had an unusually high percentage of the vote in that county, and an unusually large number of ballots (19,000) were discarded because voters had marked two circles (possibly by inadvertently voting for Buchanan and then trying to correct the mistake by then voting for Gore).

    The data in votes.txt give the numbers of votes for Buchanan and Bush in 67 counties in Florida. We will characterize the relationship between votes for Bush (X) and votes for Buchanan (Y). What statistical evidence is there that Buchanan received more votes than expected in Palm Beach County? Analyze the data without Palm Beach County results to obtain an equation for predicting Buchanan votes from Bush votes. Obtain a 95% prediction interval for the number of Buchanan votes in Palm Beach from this result assuming the relationship is the same in this county as in the others. If it is assumed that Buchanan's actual count contains a number of votes intended for Gore, what can be said about the likely size of this number from the prediction interval. (Consider transformation.)

    This problem is an example of some of the more unstructured data analysis problems you will see during the semester, particularly on the take-home midterm and on your final project. As the semester progresses, it will be assumed that you understand how to structure such a write-up of your work.

    Following are instructions that you will use for this and future 1-page write-ups.

    Put your writeup on one page maximum (11pt font, 1 inch margins [we will measure]). You will hand in two copies; the first with your name and social security number, the second with just your social security number.

    Structure of the Writeup: Use the Case Studies in the beginning of Chapters 7 and 8, as well as Homework 1, problem 1, as a guide.

    1. Introduction

      • Clear statement of research question. KEEP THIS CONCISE.

      • Description of data. If observational, how was the data collected? What was the experimental design? Mention any sampling issues (independence or possible correlation of data, sample size issues) that could have an impact on the analysis. KEEP THIS SHORT.

    2. Exploratory analysis of data: Give relevant summary statistics giving center and spread of data. These can be reported in a simple table or in a few sentences. Produce relevant plots tailored to the question at hand. Provide unique features of the data that could have an impact on the analysis: outliers, shape of distribution, sample size issues. Again, keep this very concise. If you make a table or plot, refer to it in the text. For example, you can give a regression line plot and describe the data in the plot in the exploratory analysis section, and discuss the regression line in the same plot in the statistical analysis section. Clearly label all plots.

    3. Statistical analysis. This section includes information on the statistical tests performed, and should be written in a form similar to the "Case Studies - Summary of Statistical Findings" section at the beginning of each chapter in Statistical Sleuth. For this problem, you will summarize the results of a regression performed on log-transformed data and interpret the prediction interval. Be sure to perform all relevant diagnostic tests to confirm fit of the model, and discuss the results in a couple of sentences. If you have space, you might consider plotting the prediction intervals.

    4. Summary of findings and scope of inference. To what extent does our data answer the question asked? What are the limitations of the model you have selected? Is there any problem with using the normal simple linear regression model for the purpose intended? (Are there possible block effects?) Review Section 1.2 of Statistical Sleuth. Also the "Scope of Inference" sections of the "Case Studies" should be of use here. Remember that recommending a larger sample size isn't always realistic; you will not always see perfect "textbook" datasets, and that this particular dataset may be all that is available to answer the question.