STA242/ENV255 Practice Problems for Chapter 8, not to be turned in.
  1. More practice with fitting/interpreting log transformed data.

    Crab claw size and force, #24 Sleuth, page 199, Ch. 7.

    This data comes from: Behrens Yamada, S. and E.G. Boulding. 1998. Claw morphology, prey size selection, and foraging efficiency in generalists and specialist shell-breaking crabs. Journal of Experimental Marine Biology and Ecology 220:191-211.

    Data in crabclaw.txt:

    You will only use the data for Hemigrapsus nudus which is the group with "code" variable equal to "1".

    Variables: Mean closing force (Newtons) and height (mm)

    Answer the following questions:

    1. What is the effect of a tripling of the height for the Hemigrapsus nudus? Give a 95% confidence interval for the multiplicative factor in the median.

      What are the units of b1?

    2. For each crab, closing forces were measured repeatedly, by measuring the force as the claws pulled two wires together. Could this be considered an ecological regression? Why or why not? Are their any other statistics besides the mean that might be appropriate to measure closing force?

  2. The lack of fit test.Fisk and Sammarco found that the skeletal density of the coral Porites lobata increases with distance from the Australian shore due to differences between inshore and offshore environments. The dataset, reef.txt, provides the following data for the density of Great Barrier Reef coral heads:

    1. Produce a regression line plot of Y=coral head density vs. X=distance to shore.

    2. Report the fitted regression line. In one sentence each, interpret the slope, intercept and R2.

    3. Assess lack of fit of the linear regression model by a plot of residuals vs. fitted values.

    4. Assess lack of fit of the linear regression model using the lack of fit F-test.

      • Print out the ANOVA table for the simple linear regression. You can do this by clicking the box under "Results" in the regression menu called "ANOVA table".
      • Print out the ANOVA table for a one-way analysis of variance. Before fitting the ANOVA model, you will need to go to "Data" and "Change Data Type" and change the data type for the X variable to a factor.

    5. Investigating a polynomial fit. We will now consider the following regression model:

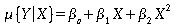
      1. First, make a plot of this fitted model for the coral reef data. Go to "Graph" - "2D Plot" - "Fit-Polynomial Curvefit". Choose the X and Y variables as before. Click on the "Curve Fitting" tab and check that you are fitting "Curve Fit Type: Linear" and "Poly. Order 2". Click "OK" to produce the plot.
      2. Next, fit the model by choosing "Statistics" - "Regression" - "Linear". In the "Formula" box, type "Density~Distance+Distance^2". Write out the fitted model.
      3. In the regression output for the fitted model, look at the p-value corresponding to "I(Distance^2)". This is the p-value for the two-sided hypothesis test of Ho: b2 = 0 in the presence of b0 and b1. That is, we are comparing the simple linear model to the polynomial model of degree 2. What does the p-value say about the polynomial model?

    Last modified: Tue Feb 10 22:23:13 EST 2004