class: center, middle, inverse, title-slide # Multiple linear regression + Model selection ### Dr. Çetinkaya-Rundel ### 2018-02-28 --- ## Announcements - HW 03 due next Monday --- class: center, middle ## Data cleaning --- ## Load data ```r pp <- read_csv("data/paris_paintings.csv", na = c("n/a", "", "NA")) ``` --- ## Shape and material Collapse levels of `Shape` and `mat`erial variables with `forcats::fct_collapse`: .small[ ```r pp <- pp %>% mutate( Shape = fct_collapse(Shape, oval = c("oval", "ovale"), round = c("round", "ronde"), squ_rect = "squ_rect", other = c("octogon", "octagon", "miniature")), mat = fct_collapse(mat, metal = c("a", "br", "c"), canvas = c("co", "t", "ta"), paper = c("p", "ca"), wood = "b", other = c("e", "g", "h", "mi", "o", "pa", "v", "al", "ar", "m")) ) ``` ] --- ## Review fixes .pull-left[ ```r pp %>% count(Shape) ``` ``` ## # A tibble: 5 x 2 ## Shape n ## <fct> <int> ## 1 other 12 ## 2 oval 52 ## 3 round 74 ## 4 squ_rect 3219 ## 5 <NA> 36 ``` ] .pull-right[ ```r pp %>% count(mat) ``` ``` ## # A tibble: 6 x 2 ## mat n ## <fct> <int> ## 1 metal 321 ## 2 other 59 ## 3 wood 886 ## 4 paper 38 ## 5 canvas 1783 ## 6 <NA> 306 ``` ] --- class: center, middle ## Review --- ## Main effects, numerical predictors ```r m_main_n <- lm(log(price) ~ Width_in + Height_in, data = pp) tidy(m_main_n) %>% select(term, estimate) %>% mutate(estimate = round(estimate, 3)) ``` ``` ## term estimate ## 1 (Intercept) 4.769 ## 2 Width_in 0.027 ## 3 Height_in -0.013 ``` --- ## Visualizing the model ``` ## Warning: Ignoring 258 observations ``` <div id="htmlwidget-4693eca3c54b81d80845" style="width:100%;height:70%;" class="widgetframe html-widget"></div> <script type="application/json" data-for="htmlwidget-4693eca3c54b81d80845">{"x":{"url":"07b-mlr-model-select_files/figure-html//widgets/widget_unnamed-chunk-7.html","options":{"xdomain":"*","allowfullscreen":false,"lazyload":false}},"evals":[],"jsHooks":[]}</script> --- ## Main effects, numerical and categorical predictors .small[ ```r pp_Surf_lt_5000 <- pp %>% filter(Surface < 5000) m_main <- lm(log(price) ~ Surface + factor(artistliving), data = pp_Surf_lt_5000) tidy(m_main) %>% select(term, estimate) %>% mutate(exp_estimate = round(exp(estimate), 4)) ``` ``` ## term estimate exp_estimate ## 1 (Intercept) 4.8800835400 131.6417 ## 2 Surface 0.0002653092 1.0003 ## 3 factor(artistliving)1 0.1372102561 1.1471 ``` - All else held constant, for each additional square inch in painting's surface area, the price of the painting is predicted, on average, to be higher by a factor of 1.0003. - All else held constant, paintings by a living artist are predicted, on average, to be higher by a factor of 1.1471 compared to paintings by an artist who is no longer alive. - Paintings that are by an artist who is not alive and that have a surface area of 0 square inches are predicted, on average, to be 131.6417 livres. ] --- ## What went wrong? .question[ Why is our linear regression model different from what we got from `geom_smooth(method = "lm")`? ] .pull-left[ <!-- --> ] .pull-right[ <!-- --> ] --- ## What went wrong? (cont.) - The way we specified our model only lets `artistliving` affect the intercept. - Model implicitly assumes that paintings with living and deceased artists have the *same slope* and only allows for *different intercepts*. - What seems more appropriate in this case? * Same slope and same intercept for both colors * Same slope and different intercept for both colors * Different slope and different intercept for both colors? --- ## Interacting explanatory variables - Including an interaction effect in the model allows for different slopes, i.e. nonparallel lines. - This implies that the regression coefficient for an explanatory variable would change as another explanatory variable changes. - This can be accomplished by adding an interaction variable: the product of two explanatory variables. --- ## Interaction: surface * artist living .small[ ```r ggplot(data = pp_Surf_lt_5000, mapping = aes(y = log(price), x = Surface, color = factor(artistliving))) + geom_point(alpha = 0.3) + geom_smooth(method = "lm") + labs(x = "Surface", y = "Log(price)", color = "Living artist") ``` <!-- --> ] --- ## Modeling with interaction effects .small[ ```r m_int <- lm(log(price) ~ Surface + factor(artistliving) + Surface * factor(artistliving), data = pp_Surf_lt_5000) tidy(m_int) %>% select(term, estimate) ``` ``` ## term estimate ## 1 (Intercept) 4.9141893558 ## 2 Surface 0.0002059164 ## 3 factor(artistliving)1 -0.1261225393 ## 4 Surface:factor(artistliving)1 0.0004792379 ``` ] $$ \widehat{log(price)} = 4.91 + 0.00021~surface - 0.126~artistliving $$ $$+ ~ 0.00048~surface \times artistliving $$ --- ## Interpretation of interaction effects - Rate of change in price as the surface area of the painting increases does vary between paintings by living and non-living artists (different slopes), - Some paintings by living artists are more expensive than paintings by non-living artists, and some are not (different intercept). .small[ .pull-left[ - Non-living artist: `\(\widehat{log(price)} = 4.91 + 0.00021~surface\)` `\(- 0.126 \times 0 + 0.00048~surface \times 0\)` `\(= 4.91 + 0.00021~surface\)` - Living artist: `\(\widehat{log(price)} = 4.91 + 0.00021~surface\)` `\(- 0.126 \times 1 + 0.00048~surface \times 1\)` `\(= 4.91 + 0.00021~surface\)` `\(- 0.126 + 0.00048~surface\)` `\(= 4.784 + 0.00069~surface\)` ] .pull-right[ 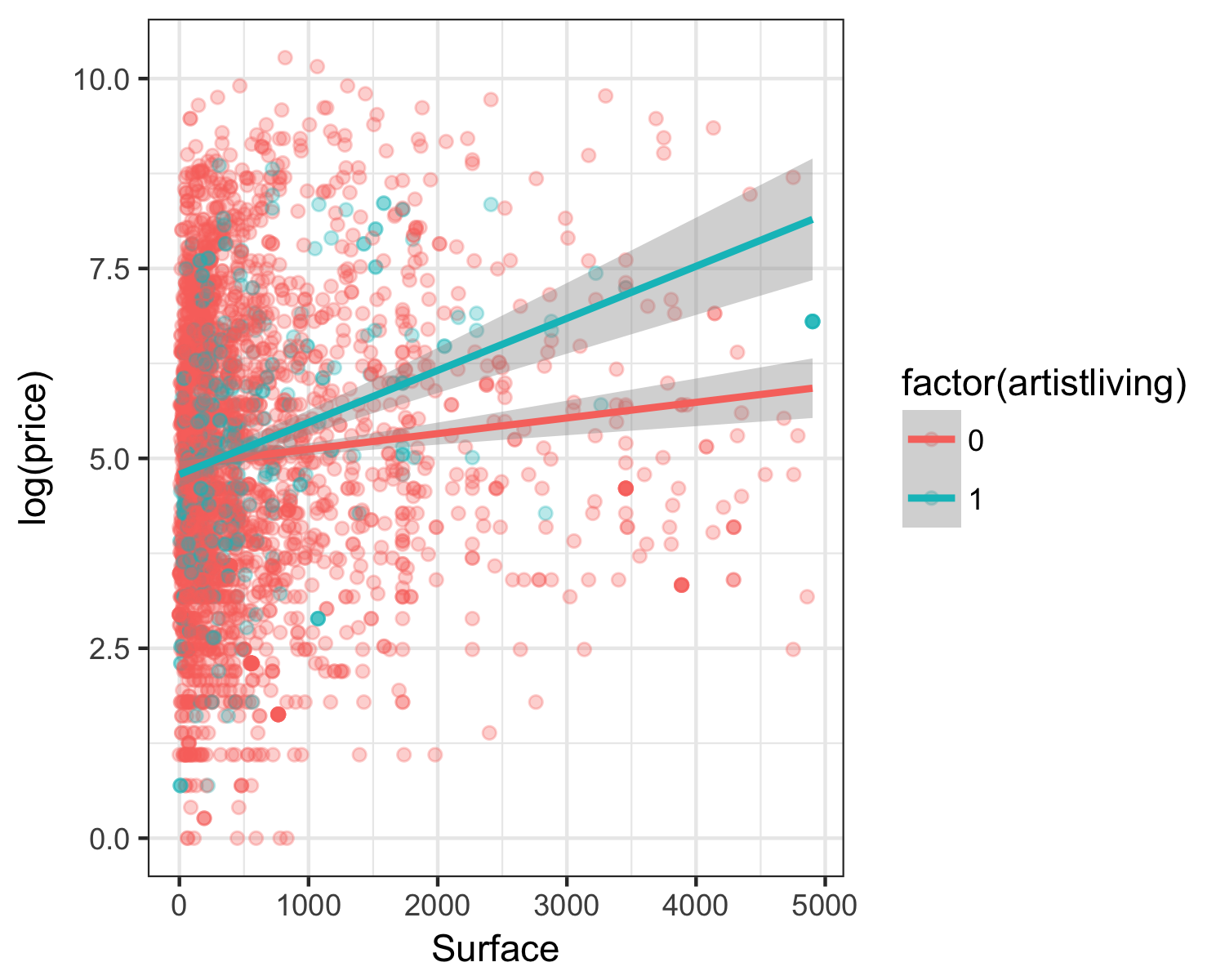<!-- --> ] ] --- ## Third order interactions - Can you? Yes - Should you? Probably not if you want to interpret these interactions in context of the data. --- class: center, middle # Quality of fit in MLR --- ## `\(R^2\)` - `\(R^2\)` is the percentage of variability in the response variable explained by the regression model. ```r glance(m_main)$r.squared ``` ``` ## [1] 0.01320884 ``` ```r glance(m_int)$r.squared ``` ``` ## [1] 0.0176922 ``` -- - Clearly the model with interactions has a higher `\(R^2\)`. -- - However using `\(R^2\)` for model selection in models with multiple explanatory variables is not a good idea as `\(R^2\)` increases when **any** variable is added to the model. --- ## `\(R^2\)` - first principles $$ R^2 = \frac{ SS\_{Reg} }{ SS\_{Total} } = 1 - \left( \frac{ SS\_{Error} }{ SS\_{Total} } \right) $$ .question[ Calculate `\(R^2\)` based on the output below. ] ```r anova(m_main) ``` ``` ## Analysis of Variance Table ## ## Response: log(price) ## Df Sum Sq Mean Sq F value Pr(>F) ## Surface 1 138.5 138.537 40.6741 2.058e-10 ## factor(artistliving) 1 6.8 6.810 1.9994 0.1575 ## Residuals 3188 10858.4 3.406 ``` --- ## Adjusted `\(R^2\)` $$ R^2\_{adj} = 1 - \left( \frac{ SS\_{Error} }{ SS\_{Total} } \times \frac{n - 1}{n - k - 1} \right), $$ where `\(n\)` is the number of cases and `\(k\)` is the number of predictors in the model -- - Adjusted `\(R^2\)` doesn't increase if the new variable does not provide any new informaton or is completely unrelated. -- - This makes adjusted `\(R^2\)` a preferable metric for model selection in multiple regression models. --- ## In pursuit of Occam's Razor - Occam's Razor states that among competing hypotheses that predict equally well, the one with the fewest assumptions should be selected. - Model selection follows this principle. - We only want to add another variable to the model if the addition of that variable brings something valuable in terms of predictive power to the model. - In other words, we prefer the simplest best model, i.e. **parsimonious** model. --- ## Comparing models It appears that adding the interaction actually increased adjusted `\(R^2\)`, so we should indeed use the model with the interactions. ```r glance(m_main)$adj.r.squared ``` ``` ## [1] 0.01258977 ``` ```r glance(m_int)$adj.r.squared ``` ``` ## [1] 0.01676753 ``` --- class: center, middle # Model selection --- ## Backwards elimination - Start with **full** model (including all candidate explanatory variables and all candidate interactions) - Remove one variable at a time, and select the model with the highest adjusted `\(R^2\)` - Continue until adjusted `\(R^2\)` does not increase --- ## Forward selection - Start with **empty** model - Add one variable (or interaction effect) at a time, and select the model with the highest adjusted `\(R^2\)` - Continue until adjusted `\(R^2\)` does not increase --- ## Model selection and interaction effects If an interaction is included in the model, the main effects of both of those variables must also be in the model If a main effect is not in the model, then its interaction should not be in the model. --- ## Other model selection criteria - Adjusted `\(R^2\)` is one model selection criterion - There are others out there (many many others!), we'll discuss some later in the course, and some you might see in another courses --- class: center, middle # Your turn --- ## Your turn Work in teams on RStudio Cloud **Project:** Model selection for Paris Paintings Make a copy and get started --- ## Planning Decide on a subset of variables to consider for your analysis. - Think about it as focusing on certain aspects of the price determination, as opposed to all aspects. - You're allowed a maximum of 10 total variables to consider, including interactions. - The more variables you consider the longer model selection will take so keep that in mind. --- ## Planning (cont.) Decide among these which variables might make sense to interact. Remember, we consider interactions when variables might behave differently for various levels of another variable. Ideally, you would get expert guidance for choosing interactions. Below is a list of interactions compiled by them that might be potentially interesting: .small[ - School of painting & landscape variables: `school_pntg` & `landsALL` / `lands_figs` / `lands_ment` - Landscapes & paired paintings: `landsALL` / `lands_figs` / `lands_ment` & `paired` - Other artists & paired paintings: `othartist` & `paired` - Size & paired paintings: `surface` & `paired` - Size & figures: `surface` & `figures` / `nfigures` - Dealer & previous owner: `dealer` & `prevcoll` - Winning bidder & prevcoll: `endbuyer` & `prevcoll` - Winning bidder & artist living: `winningbiddertype` & `artistliving` ] This is not an exhaustive list, so you might come up with others. --- ## Model fitting, selection, and interpretation - Use backwards elimination to do model selection. Make sure to show each step of decision (though you don't have to interpret the models at each stage). - Provide interpretations for the slopes for the final model you arrive at and create at least one visualization that supports your narrative.