Homework #5--Suggested Answers

ISBE 4.22, 4.29, 5.1, 5.9, 5.13, 5.17, 5.26

4.22

1. Pr(X>120) = Pr(Z>.5) = 0.309, thus the proportion of students finishing within 2 hours is 1-Pr(Z>.5) = 0.691, or 69.1%
2. 135.6 minutes. First, find the value of z such that Pr(Z>=z) = 0.1 by finding 0.1 in Table IV and identifying the associated z score, z=1.28. Use equation 4-23 to solve for X, which is 135.6.

4.29

Answers A, B, and E are true as they are linear transformations of the random variable X. In D, 10 does not equal 9. In C, 3.75 does not equal 10/3.

5.1

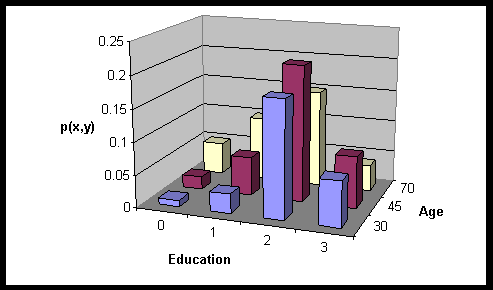
1. 7%

b.

c. No. Pr(X=3,Y=30)=0.07 does not equal Pr(X=3)*Pr(Y=30) = 0.29*0.19= 0.0551, for example.

d. m _X = 1.84 or the sum 0*.08 + 1*.19 + 2*.54 + 3*.19

s _X= .82 or the square root of the sum (0-1.84)²*.08 + (1-1.84)²*.19 + (2-1.84)²*.54 + (3-1.84)²*.19

e. As an example, here is what Excel does. You will have done this by hand, though, and it will most likely look more like figure 5-2 in the book.

5.9

1. 16.17, or the sum .4(1)²*20*.16 + .4(1)²*25*.09 + .4(1.25)²*20*.15 + .4(1.25)²*25*.30 + .4(1.5)²*20*.03 + .4(1.5)²*25*.17 + .4*(1.75)²*20*.0 + .4*(1.75)²*25*.1--formula 5-9
2. 6.6, calculation similar to 5.1 d
3. 6145, multiply average volume by number of trees (16.17*380)
4. E(D) = 1.2875, E(H) = 23.3, No

5.13

1. For part c, r = 0, as s x,y = 0. Yes, X and Y are independent (compare the joint probabilities with a table of p(x)p(y); they are the same). For part d, r = 0, as s x,y = 0. No, X and Y are not independent as the joint probabilities are not the same the values in a table of p(x)*p(y). For example, 0=Pr(x=0,y=2) does not equal Pr(x=0)*Pr(Y=2)=(1/8)*(1/2).
2. Statement (1) is true, statement (2) is false.

5.17

a.

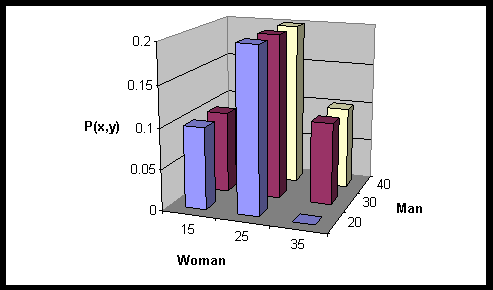
b. For the random variable X: p(X=20) = 0.3, p(X=30) = 0.4, p(X=40) = 0.3, E(X) = 30, and Var(X) = 60. For the random variable Y: p(Y=15) = 0.2, p(Y=25) = 0.6, p(Y=35) = 0.2, E(Y) = 25, Var(Y) = 40

5.26

1. Negative. When S is large, T tends to be small; when S is small, T tends to be large. Start by transforming percents to decimals; on this scale, the covariance = - 0.0008.

 

2. When investing all in stocks return, R = 10,000*S; investing all in t-bills R = 10,000*T; investing 50-50, R = 5,000*S + 5,000*T and investing 20-80 R = 2,000*S + 8,000*T. Note that E(S) = 0.09, E(T) = 0.08, SD(S) = 0.0943 and SD(T) = 0.0127. Use the formulae in Table 5-7, line 2 (page 175 of the book) to fill in the table:

 

 

Stock/Treasury Bills Split	Expected Value	Standard Deviation
100/0	900	943
0/100	800	127
50/50	850	432
20/80	820	142

 

3. 100% investment in Stocks gives the highest return, whereas the lowest risk is associated with 100% in T-bills.

 

4. No, expected return is highest with all resources devoted to the instrument (stocks) of highest return.

 

5. Yes. Note that E(R) = 10,000*(a*E(S) + (1-a)*E(T)), that is, expected return is a linear combination of return on stocks and return on T-bills. The constant "a," which ranges from 0 to 1, determines the fraction invested in stocks. This expression can be re-written E(R) = 10,000*(a*(E(S)-E(T)) + E(T)). Filling in the values for E(T) and E(S), we get E(R) = 100*a + 800, the equation of a line with positive slope. E(R) is maximized by choosing as large a value for "a" as we can, i.e. a=1, corresponding to all money in stocks.

 

6. Yes, risk is typically lower with a mix of two negatively correlated investments (when one goes down, the other tends to go up, compensating losses). Risk should be smallest with somewhere between 0 and 20% in stocks.

 

7. The ratio is (var(T) - cov(S,T))/(var(S) - cov(S,T)) = 10. Hence a ratio of 10-1 investment in favor of T-bills (1/11 in stocks, 10/11 in T-bills) has lowest risk (SD(R) = 86).

 

8. was not; all in stocks ; 1/11th in stocks; careful evaluation of.