NOTE: These are just random questions from some previous exams for you to practice on. They are not intended to precisely reflect the actual difficulty, length, or scope of your exam. They do not come with a warranty! Your exam's actual mileage may vary.

1. Scores on an exam are normally distributed with a mean of 70 and a standard deviation of 6.

(a) What percentage of the class got a score higher than 72?

(b) The professor only wants to give an "A" to students scoring at or above the 90th percentile. What is the numerical cutoff for an "A"?

(c) Bill's z-score on this exam was -1.5. What was his raw (actual) score?
 
 
 
 

2. Would you expect positive skew, negative skew, or no skew at all for the following data sets or distributions?

(a) Data set with mean=15, median=25

(b) Data set containing personal incomes in the U.S.A.?

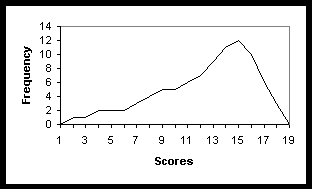
(c) Look at the histogram below, and answer d1, d2, and d3:

Yet new studies suggest that despite the promulgation in 1991 of a Federal plan to reduce to almost zero the amount of lead that can enter the bodies of unborn and young children, an estimated 3 million pre-school age American children currently harbor more that 10 micrograms of lead.

Dr. John Rosen, a pediatric specialist on lead poisoning, says the highest prevalence of silent lead poisoning occurs in African-American children who live in large cities and whose families have marginal incomes. One-third of these children have hazardous amounts of lead in their blood and only 6 percent of white children living under similar circumstances have the same levels. The reasons for these differences are not known, but they could reflect genetic or dietary differences among the different groups.

The preponderance of evidence suggests that low levels of lead can harm the brains of young children. For example, newly published findings suggest that lead damage to children’s developing brains could make the difference between their being on the low end of normal intelligence and dropping below normal.

In a continuing study of 170 children from middle-and upper-middle-class families in Boston, Dr. David Bellinger found significant signs of lasting brain damage in children even in low-risk environments. For every 10 micrograms of blood lead above the 10-microgram danger level measured when the children were 2 years old, he found a 5.8 point decline in overall IQ by age 10.

The following questions pertain to Dr. Bellinger’s study:

4. (Fictional study.) A researcher selected a random set of employees to test the hypothesis that drinking more coffee makes a person feel more alert and think faster. For each subject, the researcher would pick a random morning and interview the subject at 10 a.m., asking him/her how many 8oz cups of coffee he or she had. The researcher also administered a test of alertness to the subject and noted his/her score.

(a) Was this an observational study or a controlled experiment?
 
 

(d) Assume that the scatterplot below summarizes the researcher's results

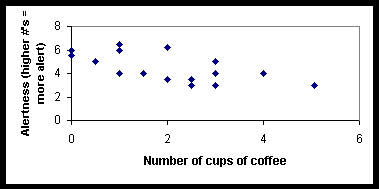
a) Is the correlation between amount of coffee drunk and alertness likely to be closer to:

0.0, 0.2, -0.1, 0.8, or -0.8?

2. The results tend to go in the opposite direction predicted by the researcher. Do these results offer strong evidence that coffee drinking decreases alertness? If so, why? If not, how else could the results be explained?

5. Physical exercise is considered to increase the risk of spontaneous abortion. Furthermore, women who have had a spontaneous abortion are more likely to have another. One observational study finds that women who exercise regularly have fewer spontaneous abortions than other women. Can you explain the findings of this study?

Student:       a   b   c   d   e

No. absences: 10, 12,  2,  0,  6

Final Grade:  70, 65, 96, 94, 75

a.Give the mean and standard deviations for final grades and and number of absences.

b. Give the z scores for final grades and absences.

c. What is the value of correlation between absences and grades?

d. What percent of variation in final grades is accounted for by the relationship between absences and grades?

e. Give the regression equation (predict final grades using number of absences)

f. Based on this equation, how much (and in what direction) will the final grade change for each additional absence?

g. Based on this equation, if a student has zero absences, what would be his or her predicted grade?
 
 

We discussed four different measures of variability. Name three of them and give an advantage or disadvantage of each.
 

What is a normal quantile plot used for and how do you read it?
 

A lot of lines could be considered to "fit" a set of points on a scatterplot.  How is "best fit" defined for the least-squares regression line?