Note 1: Exam has been moved to Thursday. No class on Tuesday. (Students who want to take the exam on Tuesday need to show up at the regular class time.)

Note 2: These are just some exam questions for you to practice on. The exact difficulty and make-up of your actual exam may vary.

Practice Exam

1) Assume that you are applying for three jobs, one with the firm of Smith, Carlyle, and Snookums, one with the firm of Dewy, Cheatham, and Howe, and the last with the firm House of Pancakes. Assume the probability that you get a job offer from Smith et al. is 0.3, the probability of getting an offer from Dewey et al. is .6, and the probability of getting an offer from House et al is 0.8.

a) What is the probability that you will get a job offer from Smith et al or Dewey et al?

b) What is the probability that at least one job offer if you apply at all three firms.

c) For this part of the question forget about the House et al job. Consider only the Smith and Dewey jobs. Assume that you prefer to work at Smith., and will take that job if offered. If you aren't offered a job at Smith, but are offered one at Dewey you will take the Dewey job. What is the probability that you will end up working at Dewey et al?

2) (Challenging.) A brand of flashlight battery has normally distributed lifetimes with a mean of 30 hours and a standard deviation of 5 hours. A supermarket purchases 500 of these batteries from the manufacturer. What is the probability that at least 80% of them will last longer than 25 hours?






3) Consider a random variable X whose population distribution is given by the following probability histogram:

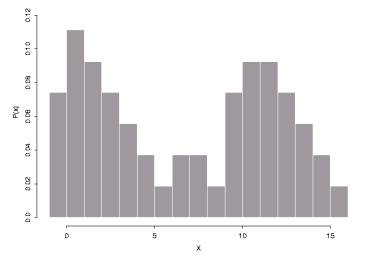
The mean and standard deviation for this population (assume the population is infinite) are given as follows:

m_x= 7.22 ; s _x = 5.11

(a) For a random sample of size n = 147 from this population, the Central Limit Theorem can be used to determine the (approximate) sampling distribution of the sample mean. State the shape of this distribution, and provide its mean and standard error.

(b) Now, pretend that the mean of the above mentioned population is unknown. For the random sample of size n = 147 above, you find that the sample mean is 6.33. How far off would you expect this estimate to be from the true population mean

(c) Knowing what the real population mean is, do you think the value of the sample mean you observed in (b) is unusual? Briefly support your answer.

4) In a family of 8 children, what is the chance that there will be exactly two boys? Assume that the gender of each child is equally likely to be male or female. (This is not a trick or a paradox! It is a straightforward probability problem.)

5) In a certain city, 80% of all drivers have auto insurance. Those who have auto insurance have a 2% chance of being involved in an accident, while those drivers without insurance have an accident rate of only 7%. Suppose a driver hits you. What is the probability that this driver has auto insurance?

6) Which hypothesis- the null or the alternative- is the researcher usually most interested in supporting? Which hypothesis does he end up testing? Why?

7) If you change alpha from .05 to .10, what effect will that have on the power of your study?

8) Mary believes that brown-eyed women like her tend to be smarter than the average person. She randomly selects 5 brown-eyed women and gives them an IQ test. Their IQ. s are: 105, 112, 98, 122, and 103. Is this evidence enough to show intelligence superiority for brown-eyed women, that is, that their mean IQ is different than the national mean of 100? (Use a = .05.)

9) Compute the 99% confidence interval for the mean IQ of brown-eyed women based on the data from question 8.

10) What are sampling distributions and what use are they?

11) What is the difference between a standard deviation and a standard error?

12) You read a newspaper article that states that researchers have found that daily meditation causes a decrease in blood pressure for people with high blood pressure. Assume that the researchers did an excellent job of designing a flawless double-blind experimental study with a very large, representative sample, and their results were significant for a = .01. Could you legitimately conclude that meditation is an effective intervention for high blood pressure? If so, why? If not, what additional information would you want?

13) If the random variable X has a m = 10 and a s =5, and the random variable Y has a m=20 and a s = 5, what are the values of m and s for the random variable Z = X -Y? What about for the random variable V = X + Y?